Curation is a form of good teaching. Great teachers provide just the right number of deliberate materials to ensure that the student has ample supply to learn, but not too many to be distracted. That said, having lots of something is not only a terribly exciting prospect for young people, but may be necessary for deep learning.
As soon as a child can count, they want to count more things, resulting in ever bigger numbers. Part of the allure of the Logo turtle is that you can command it to go forward 99999 steps or repeat something 1 million times. This is powerfully seductive for children playing with big numbers. Kids love to collect lots and lots of things. Abundance can be quite motivating.
When used as a goal, lots can unlock creativity and help overcome the obstacles of imagination. During a conference about the Reggio Emilia approach, we were tasked with identifying one hundred things one could weave. My immediate reaction was, “No way!” Then we began weaving strips of fabric, string, tree branches, plastic bags, yarn, coat hangers… and before long we had a list of more than one hundred things to weave. The audacious goal of “lots” expanded our imaginations.

High School Maths
The other day, I was invited to lead a brief PD session for the maths faculty of a public high school in suburban Melbourne, Australia. I knew none of the teachers except for a vice principal who was a friend of a friend that I met a few nights earlier socially. I always face high school maths teachers with a bit of healthy trepidation based on my own terrible experiences as a student and an awareness that maths teaching is the one part of a school inconsistent with my objectives as an advocate for constructionist learning. (include link to my story and constructionism)
I made a short presentation about the need for reforming mathematics education, the need for learning-by-making, and the case for developing computational fluency – leaving enough time for a quick activity and discussion of some computational problems I’ve been exploring personally and with kids.
As I made the segue into introducing the “Hailstone” or “Collatz” problem, the teacher perked up and told me, “We already do that!” The voice in my head, “I are so screwed.” I managed to maintain my composure and asked the teachers a few questions:
- How many of you know the problem we’re talking about?
- Why do you teach that problem?
- How do you teach that problem?
About 25% of the teachers were familiar with the problem. They explained that they use it to teach conjecture and told me that they use pencil and paper to explore the problem.
I was no longer scared
The Hailstone/Collatz/3N+1 problem is a fun number theory investigation that only requires rudimentary arithmetic to engage in the habits of a mathematician. If you put a positive integer into a machine, it encounters just two rules.
- If the number is even, cut it in half.
- If the number is odd, multiply the number times 3 and add 1 (3n+1)
Next, that new value is put back through the machine until a repeating pattern of 4…2…1… appears. Every positive integer is eventually reduced to that repeating pattern. The fun part is predicting how a number will behave.
Performing this arithmetic is fine and dandy until one encounters the number 27. 27 “feels” like a normal number, but it takes 109 generations (iterations) to reach the repeating pattern of 4…2…1…
Here is where the conjecture comes in. What is it about 27 that causes such strange behavior?
Once my students stumble across 27, I ask questions like, 27 moved in next door. What’s she like? This anthropomorphization invites learners to think about traits of a number, explore its qualities, and offer a conjecture as to what makes it unique. 109 generations is a LOT more than the number of generations associated with other small numbers. (The idea of limits and orders of magnitude creep into the classroom).
I’ve seen students identify traits such as:
- It’s greater than 10
- It’s odd
- The sum of its digits = 9
- Both digits are prime
- It’s a perfect cube, etc…
Instead of telling students that this is a lesson on conjecture, defining conjecture, and giving them a pencil and paper exercise in making conjectures, I introduce this “problem,” with a grandiose statement, “Welcome world’s most prominent mathematicians!” This problem provides fertile ground for what David Perkins calls, creating “a junior version of the whole game” in which students will be mathematicians rather than being taught math.
(I should confess that I didn’t understand that the point of a mathematical proof was to “prove” something until about 20 years after high school. In math class, I came to understand a proof as a whole bunch of syntactical mumbo-jumbo that I needed to memorize for a test and then never use again.)
One goal of our mathematics convention is to make statements/hypotheses/conjectures and for everyone else to confirm or debunk your thinking. This makes for a lively classroom where mathematics comes alive. In this spirit, it is easy to disprove the first few conjectures in the list above, all while using language to explain mathematical abstractions. However, perfect cube is interesting.
Let’s test the next perfect cube… 64
No luck. 64 only takes 4 generations
OK, I’ll modify my hypothesis. How about 125? (5 cubed)
105 takes 106 generations!!!
“OK! OK! I got it says a student”
“Odd perfect cubes take a long time.”
Now, our room full of mathematicians need to find an odd perfect cube that doesn’t take a long time or an even perfect cube that does, but man ‘o man that requires a lot of hand calculation… If only someone had a…
Computer! That’s what we need!
Playing with this problem with numbers < 30 is cute, but it barely scratches the surface.
Surely, we can check many even and odd perfect cubes looking for anomalies.
What if we could write a computer program to do this for us?
What if we could build a tool that would run all-night and record numbers that behave in interesting ways?
Kids should be able to write programs like that in languages, such as Logo, but sadly too few possess such skill and there is little time in math class for – well, mathematics.
So, I’ve written a tool for you in Lynx, a web-based version of Logo. You could also do so in Snap! (Find exploration of the tool at https://constructingmodernknowledge.com/3n) Think of this as a bit of scaffolding, but don’t give up on the idea of kids developing sufficient computational fluency to build their own tools.
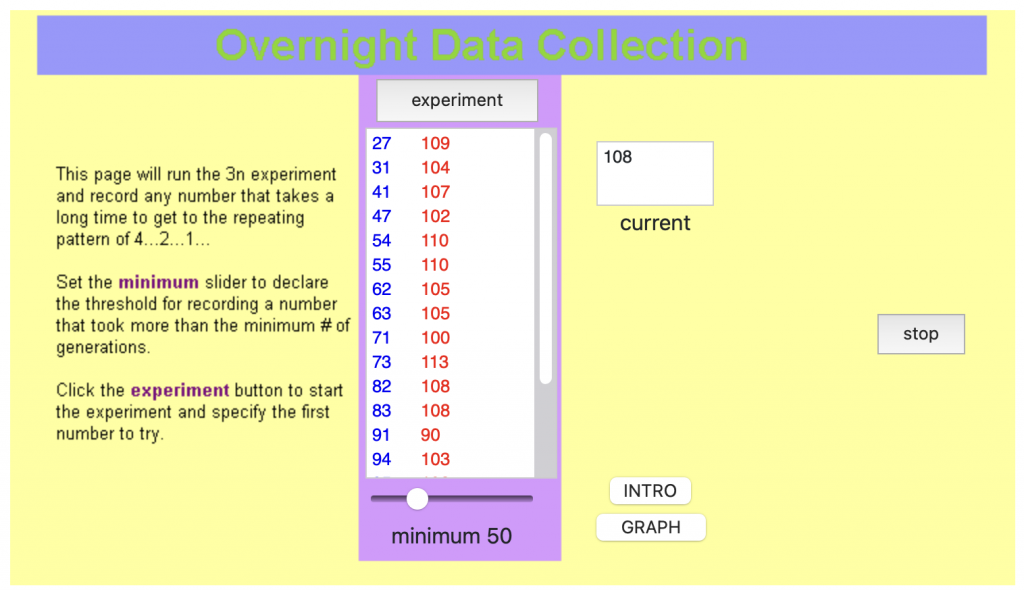
The inefficiency and tyranny of the pencil causes the teachers I work with to stop at the number, 30. This sadly aborts the wondrous possibilities of finding patterns, making sense of data, and understanding conjecture as a consequence of experience.
For example, take a look at the overnight tool screenshot above. I set a threshold for defining “long time” at 50 and asked my computerized lab assistant to test each number starting at an initial value and record any number that takes longer than that threshold number of generations to reach the repeating pattern. 54 looks familiar. It’s 2X 27. So naturally, if 27 took 109 generations, 54 will take 110 generations – one more.
Wait! Wait! Wait! Look at 55! It’s adjacent to 54 and not only also takes a long time, but the exact same long time. Whoa!
62 & 63
82 & 83
Same deal!
Run the experiment a bit longer and see if you find triple adjacent numbers taking the same long time. What about if we start looking above 1,000? Does this have anything to do with place value? How would you find out? (I had a kid debunk a conjecture I was happy with for many years.)
Another view of the data
Perhaps we should look at the behavior of this problem in a different way. Again, one should be able to program their own software for graphing the data, but my tool will do that too.
What if we graph the experimental data?
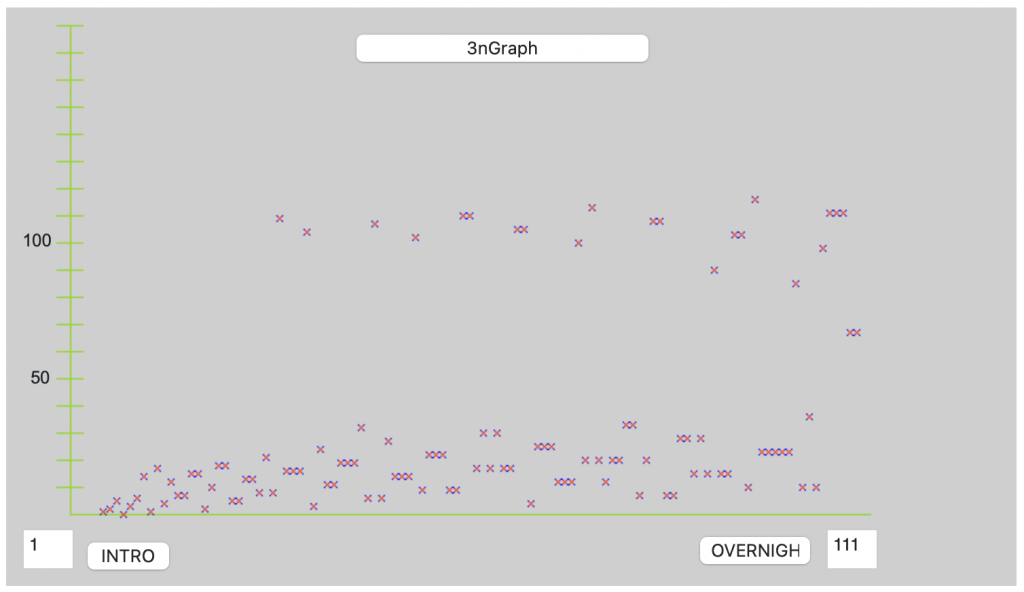
What do the X and Y axes represent?
Ever see a graph like this before?
What story does this graph tell?
Does the picture change with larger numbers?
The perfect lab assistant
The computer/software combination serves as the perfect lab assistant. It doesn’t need to sleep, eat, or be paid. It will work all night – weekends too. Best of all, it provides valuable assistance in allowing mathematicians such as yourself to think, observe patterns, test hypotheses, share findings, and disprove the conjectures of your peers – all without doing any of the thinking for you.
It turns out that the new generative AI chatbots are pretty good at writing software in languages like Python or Javascript for creating laboratories like this. You can even ask for the HTML in which to embed the programs as interactive web pages.
A magician never reveals his tricks
I will refrain from telling you how I normally end this activity with students. (Hint: It is mind-blowing.) If you want to learn more, you should invite me to lead a workshop.
Sadly, I admit to rush kids and cut the learning adventures short when constrained by the artificial limitations of schools and conferences. I have little doubt that students could pursue such mathematical inquiry longer than a class period, perhaps weeks, months, or more.
What’s the big idea?
Lots!
The computer and the act of computation dramatically enhances mathematics learning in the case of this problem and an infinite number of other cases by affording learners of all ages with a sufficient quantity of data to make sense, understand conjecture, formulate and disprove conjectures, create multiple representations, explore iteration, recognize integers, build tools, and be playful with number.
None of this is possible without the presence of the computer, computational fluency, and LOTS of numbers.
What sorts of non-computing activities benefit from abundance?
Veteran educator Gary Stager, Ph.D. is the author of Twenty Things to Do with a Computer – Forward 50, co-author of Invent To Learn — Making, Tinkering, and Engineering in the Classroom, publisher at Constructing Modern Knowledge Press, and the founder of the Constructing Modern Knowledge summer institute. He led professional development in the world’s first 1:1 laptop schools thirty years ago and designed one of the oldest online graduate school programs. Gary is also the curator of The Seymour Papert archives at DailyPapert.com. Learn more about Gary here.
