Real Inequality (not that kind)

Today, I witnessed the most exciting student outburst while teaching an online class for kids 2,000 miles away.

Oh, I know what’s wrong! It’s not greater than, it’s less than!

4th grader

In today’s synchronous session of my Clever Computing for Kids course, I introduced the class to physical computing via the BBC micro:bit. Despite a few technical glitches due to a mélange of random Chromebooks, cables, micro:bits, and the “Max Headroom” platform we’re using, the kids took to programming in MakeCode and downloading their programs to the micro:bit quite instantly. Photos snapped from behind students demonstrate understanding because I can observe examples of kids generating new ideas from what I shared with the tiniest bit of instruction.

Why am I so excited?

Anyone who has heard me speak about math education knows that I am critical of “math” being taught as a series of vocabulary terms to memorize absent any meaningful context for experiencing powerful ideas. All of my work is rooted in the Piagteian notion that “knowledge is a consequence of experience.” There is no substitute for experience. I am annoyed by how often nothing or an impoverished experience is offered when authentic ones are readily available.

Mathematics is a way of making sense of the world and computer programming is a way of making mathematics. However, far too much of the existing math curriculum and the pedagogy employed to “deliver it” have no application outside of computing. There is a fallacy of concepts building upon one another when concept development is rendered impossible due to a lack of meaningful experiences. So, we are left with vocabulary lists – denominator, quotient, obtuse, isosceles, absolute value… – terms that can be easily tested even when actual learning remains elusive.

If our objectives were no more ambitious than kids scoring better on math standardized tests, we would teach every student to program computers, preferably in a Logo-like environment. Programming is an excellent context for empowering mathematical experiences.

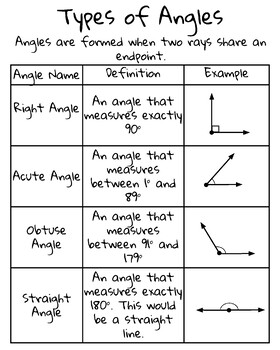
It’s hard to find a fifth grade classroom without a chart on the wall identifying the X types of angles ignoring the fact that very few children have any actual experience with angle. A few hours of programming a Logo turtle provides learners of any age with more angle fluency and understanding than years of formal instruction. Once kids experience turning the turtle to achieve their objective, you can “hang” the vocabulary onto the experience with great efficacy. Otherwise, you can teach them and teach them and teach them, but they may never stay taught.

I worked in a school where the fifth grade teacher had written, “learn numerator and denominator” on the whiteboard so long ago that it was now impossible to erase. You would have to chip the writing off with a razor or buy a new whiteboard to rid the classroom of that “math” reminder. Nine months into the school year I lost my patience and announced, “I will take out to lunch any kid who writes a program in MicroWorlds (a multimedia version of Logo, now online as Lynx) that draws any fraction as parts of a circle.” One little girl asked if they could work together, as always I replied, “yes.” The next day, three girls showed me the Logo program they created to take any fraction and create a graphic representation of it as parts of a circle.

What really irritates me is the pervasive myth that project-based learning is inefficient or a reward for surviving the drudgery of instruction. This could not be more wrong. Nearly a school year, perhaps more, had been wasted trying to get kids to memorize if numerator or denominator were the top or bottom numbers in a fraction. For what?

Spending a few hours writing a dozen line Logo program demonstrates a much greater understanding of fractions, plus division, radius, circumference, percent, variable,Euclidean geometry, order of operations, debugging, and a host of other concepts than forcing kids to “learn” two words. If students flipped a coin, they would have answered correctly more often! While programming the computer to draw fractions, the students committed the terms, numerator and denominator, to the computer’s memory while they used those terms as variable inputs to their procedures. More was learned more deeply in less time through this simple programming project. This is but one of countless examples of the limits of instruction.

I once observed a teacher at an elite private school present a breathless 43-minute lecture on absolute value to a room full of barely conscious sixth graders. After class, I asked the teacher, “Where would you use absolute value?” She thought hard for a moment, shrugged, and replied, “perhaps in seventh grade.” She was absolutely correct. There is no use for absolute value when relegated to paper and pencil. However, if you are trying to program a robot to navigate unfamiliar terrain or land your video game spaceship on a planet, absolute value comes in pretty handy.

…which brings us back to today

School is the only place where anything is ever equal to anything else. Scientists, mathematicians, engineers – hell, even musicians, carpenters, artists, or philosophers trade in inequality except in the rarest of circumstances. One is typically off by a little, within range, or close enough. Inequality is one of the most powerful ideas of science and mathematics, yet students are again subjected to a denatured paper and pencil context.

I have literally encountered teachers who while trying to determine whether they should use > or < in a computer program they’re writing to control a robot they’re inventing scrunch up their faces and try to remember if the “crocodile’s mouth is this way or that way.” That’s right, mathematical inequality is frequently taught via a Mnemonic device of remembering which way a crocodile’s head is pointing. When you program computers, that crocodile is pointed at your ass. The evaluation of inequality is critical to any logical programming.

In today’s class, I showed the kids how to determine a numerical value for the ambient light detected in a room. We spoke briefly(1) about reaching consensus for a sensor value to serve as a threshold and whether darkness would be numerically above or below that threshold. The kids then constructed their own program to check light levels and illuminate their micro:bit, or even display an animation of fireworks, when the room was darkened.

So, that’s why I was overjoyed when a fourth grader faced with his invention not working debugged his own program on-the-fly and exclaimed, “Oh, I know what’s wrong! It’s not greater than, it’s less than!”

---

Notes:

(1) 4th grade kids entered the classroom, booted their Chromebooks, were introduced to the micro:bit, challenged to write and download several simple programs to the micro:bit, encountered conditionals for the first time, used MakeCode for the first time, used a sensor for the first time, used a variable and constant in an If Else statement, and programmed their nightlight/fireworks display in 50 minutes before being rushed off to their next fabulous activity. I was teaching via Zoom projected at the front of the classroom. Several teachers were in the room to troubleshoot hardware hiccups. Thanks to them for their support and enthusiasm!

About the essay title: Sure the title of this essay is click-bait and has nothing to do (directly) with oppression, systemic racism, gender, economic, or other forms of social inequality. That said, disadvantaged students are most likely to be deprived of educationally nutritious experiences like those described here. Far too many kids are fed a STEM diet of vocabulary memorization divorced from opportunities for authentic knowledge construction.